C# Math class
What is math class?
C# math provides constants and static methods for trigonometric, logarithmic, and other common mathematical functions. The Math library in C# gives programmers access to a number of general, trigonometric, statistical, and logarithmic mathematical functions and properties. This library is plug-and-play and ready to use. The library derives from Csuper #’s parent class, the Object class. The System namespace is where it sits.
Mathematical properties in C#
E4
In mathematical equations, the little letter “e” designates the logarithmic base, which is known as E. The value of the natural logarithmic base is stored in this static attribute.
Code example:
using System;
public class Program
{
public static void Main()
{
Console.WriteLine("The value of logarithmic base E is " + Math.E);
}
}
Output:

PI
The reciprocal of the ratio of a circle’s circumference to its diameter is known as pi, which is often written as the letter p. (roughly 3.14). The value of p is contained in this static constant.
Code example:
using System;
public class Program
{
public static void Main()
{
Console.WriteLine("The value of PI is " + Math.PI);
}
}
Output:

Functions on C# Math
Abs-Absolute Function
Returns a given number’s absolute value (integer, decimal, floating-point, etc.). The highest conceivable decimal value that is higher than or equal to 0 but less than or equal to the number itself is the absolute value of any number.
Code example:
using System;
public class Program
{
public static void Main()
{
int num1 = 231;
double num2 = -1.23456789;
Console.WriteLine("The absolute value of {0} is {1} ", num1, Math.Abs(num1));
Console.WriteLine("The absolute value of {0} is {1} ", num2, Math.Abs(num2));
}
}
Output:
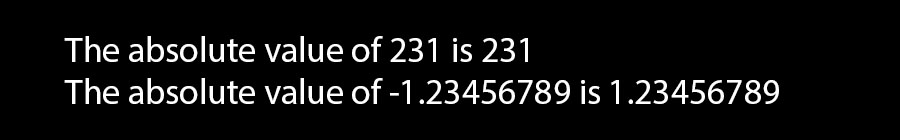
BigMul-Big Multiplication
This function delivers the entire result of multiplying two extremely large integer numbers. It requires two 32-bit integer inputs and outputs a 64-bit result of the multiplication.
Code example:
using System;
public class Program
{
public static void Main()
{
int num1 = Int32.MaxValue;
Console.WriteLine("Multiplication of {0}x{0} without Math function - {1}",num1, num1*num1);
Console.WriteLine("Multiplication of {0}x{0} by Math BigMul function - {1}",num1, Math.BigMul(num1, num1));
}
}
Output:
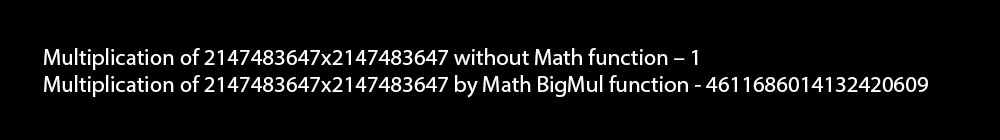
Floor and Ceiling
The floor() and ceiling() functions provide back a number’s floor and ceiling values. Any number’s floor value is its greatest integer that is less than or equal to 1. The smallest integer larger than or equal to the given number is the ceiling value of any number.
Code example:
using System;
public class Program
{
public static void Main()
{
double num1 = 548.65;
Console.WriteLine("Floor value of {0} is {1}", num1, Math.Floor(num1));
Console.WriteLine("Ceil value of {0} is {1}", num1, Math.Ceiling(num1));
}
}
Output:

Sin, Cos and Tan
The sine, cosine, and tangent values of the supplied angle are provided by these trigonometric functions.
Code example:
using System;
public class Program
{
public static void Main()
{
double angle = 120.5;
Console.WriteLine("Sine value of {0} is {1}", angle, Math.Sin(angle));
Console.WriteLine("Cosine value of {0} is {1}", angle,Math.Cos(angle));
Console.WriteLine("Tangent value of {0} is {1}", angle, Math.Tan(angle));
}
}
Output:

Tanh–Hyperbole, Cosh and Sinh
The hyperbolic sine, cosine, and tangent values of the specified angle are provided by these trigonometric functions.
Code example:
using System;
public class Program
{
public static void Main()
{
double angle = 120.5;
Console.WriteLine("Hyperbolic Sine value of {0} is {1}", angle, Math.Sinh(angle));
Console.WriteLine("Hyperbolic Cosine value of {0} is {1}", angle, Math.Cosh(angle));
Console.WriteLine("Hyperbolic Tangent value of {0} is {1}", angle,Math.Tanh(angle));
}
}
Output:
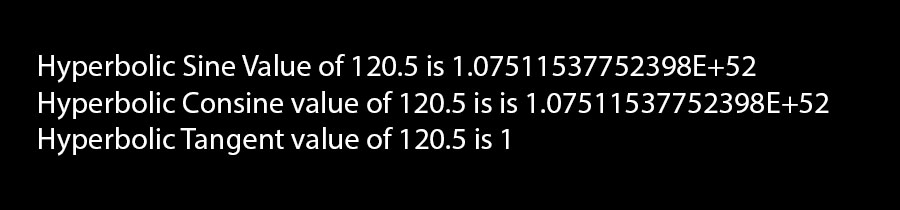
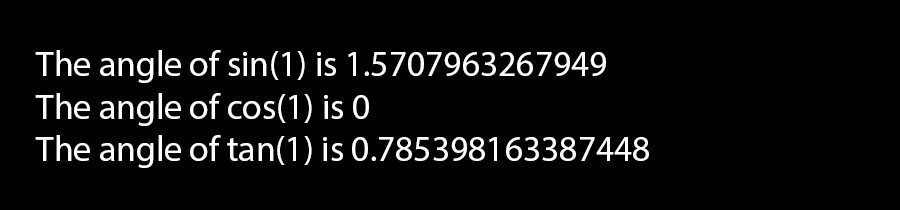
Atan, Acos and Asin
The angles to which the supplied number is the sine, cosine, or tangent value are returned by these trigonometric functions.
Code example:
using System;
public class Program
{
public static void Main()
{
double value = 1;
Console.WriteLine("The angle of sin({0}) is {1}", value, Math.Asin(value));
Console.WriteLine("The angle of cos({0}) is {1}", value, Math.Acos(value));
Console.WriteLine("The angle of tan({0}) is {1}", value, Math.Atan(value));
}
}
Output:
Remainder and DivRem–Division
This function figures out the outcome of dividing two numbers. A fractional value is not included in the returned result. Instead, the function’s return value is the quotient, and the remaining value is returned as an output parameter.
Code example:
using System;
public class Program
{
public static void Main()
{
int divisor = 8;
int dividend = 45;
int remainder = 0;
int quotient = Math.DivRem(dividend, divisor, out remainder);
Console.WriteLine("{0} divided by {1} results in {2} as the quotient and {3} as the remainder.", dividend, divisor, quotient, remainder);
}
}
Output:

Log, Log2, & Log10-Logarithm
The log function returns the base-specific logarithm of a given number. The natural logarithm is produced if no base is supplied; the default base is e.
Note that Log2 was made available in .Net Core. the .Net Framework does not have this technique.
Code example:
using System;
public class Program
{
public static void Main()
{
double num1 = 4.5;
int new_base = 12;
Console.WriteLine("Log({0}) to the base 'e' is {1}.", num1, Math.Log(num1));
Console.WriteLine("Log({0}) to the base 10 is {1}.", num1,Math.Log10(num1));
Console.WriteLine("Log({0}) to the base 2 is {1}.", num1,Math.Log(num1, 2));
Console.WriteLine("Log({0}) to the base {1} is {2}.", num1,new_base, Math.Log(num1, new_base));
}
}
Output:

Round
The round() function rounds a provided number to the nearest integer or to a specified number of decimal places after the integer, as the name implies.
There are several significant modifications to the round() function. Either two or three arguments are required.
- The amount to be rounded is the first input.
- The amount of digits following the decimal point is the second input. The number is rounded to the nearest integer if this is not given.
- The mode of rounding is the third argument. This is a list of two values that were taken from the enumeration MidpointRounding.
There are two modes:
- AwayFromZero: A number is rounded to the next number that is farther from zero when it is midway between two numbers.
- ToEven: A number is rounded to the next even number when it is exactly halfway between two numbers.
The mode AwayFromZero is the default mode if it is not provided.
Code example:
using System;
public class Program
{
public static void Main()
{
double num1 = 2.45;
double num2 = 24.5;
Console.WriteLine("{0} rounded to the nearest integer is {1}", num1, Math.Round(num1));
Console.WriteLine("{0} rounded to the nearest single-point decimal is {1}", num1, Math.Round(num1, 1));
Console.WriteLine("{0} rounded to the nearest single-point decimal away from zero is {1}", num1, Math.Round(num1, 1, MidpointRounding.AwayFromZero));
Console.WriteLine("{0} rounded to the nearest single-point decimal to even is {1}", num1, Math.Round(num1, 1, MidpointRounding.ToEven));
Console.WriteLine("\n{0} rounded to the nearest integer away from zero is {1}", num2, Math.Round(num2, MidpointRounding.AwayFromZero));
Console.WriteLine("{0} rounded to the nearest integer to even is {1}", num2, Math.Round(num2, MidpointRounding.ToEven));
}
}
Output:

Min & Max
These operations compare the two supplied numbers and output the smaller or greater of the two.
Code example:
using System;
public class Program
{
public static void Main()
{
double num1 = 4.5;
double num2 = -3.4;
int num3 = 981;
int num4 = 123;
Console.WriteLine("Minimum of {0} and {1} is {2}.", num1, num2,Math.Min(num1, num2));
Console.WriteLine("Maximum of {0} and {1} is {2}.", num1, num2,Math.Max(num1, num2));
Console.WriteLine("Minimum of {0} and {1} is {2}.", num3, num4,Math.Min(num3, num4));
Console.WriteLine("Maximum of {0} and {1} is {2}.", num3, num4,Math.Max(num3, num4));
}
}
Output:

