Binary Search Tree in Python (BST)

In this review, you will grasp more information about Binary search trees (BST). There will also be instances of BST in Python. Before starting to learn it, you need to familiarize yourself with what a Binary search tree is.

Python binary search tree uses a data structure that lets us keep values in a sorted list. Here each node is variable and this variable is bigger than its left child nodes. It is called binary sort in python.

There exists two reasons why this tree structure Python is called a Binary search tree. Firstly, each tree node has a max amount of child nodes of two (so that is why it is called a binary tree). Secondly, in O(log(n)) time search binary tree Python can be used to find a number (so that is why it is called a search tree).

The qualities that Binary search tree in Python has, and which make them different from regular binary trees:

Nodes which count as lower than the root node can be found in a node’s left subtree.
Nodes which count as bigger than the root node can be found in the right subtree of a node.
The both subtrees must be Binary search trees and possess the aforementioned characteristics.
There cannot be any duplicate nodes in binary search trees.

A tree has a right subtree with one value smaller than the root is shown to demonstrate that it is not a valid binary search tree program in Python

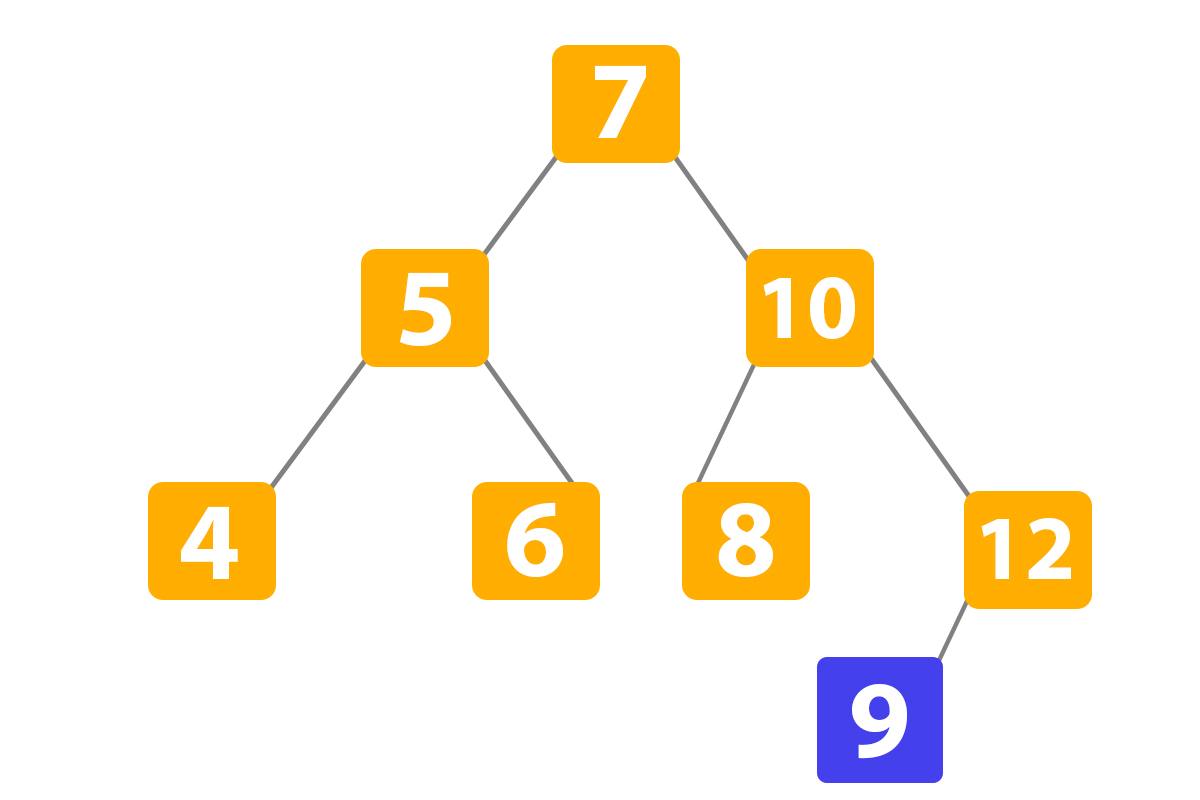
The binary tree above isn’t a valid Python binary search tree because the node “10” right subtree contains a value “9” that is smaller than it. The second property of BST Python is violated. But if we change the value “9” to “11”, it will be a Binary Python search tree. So let’s explain binary search tree with example:

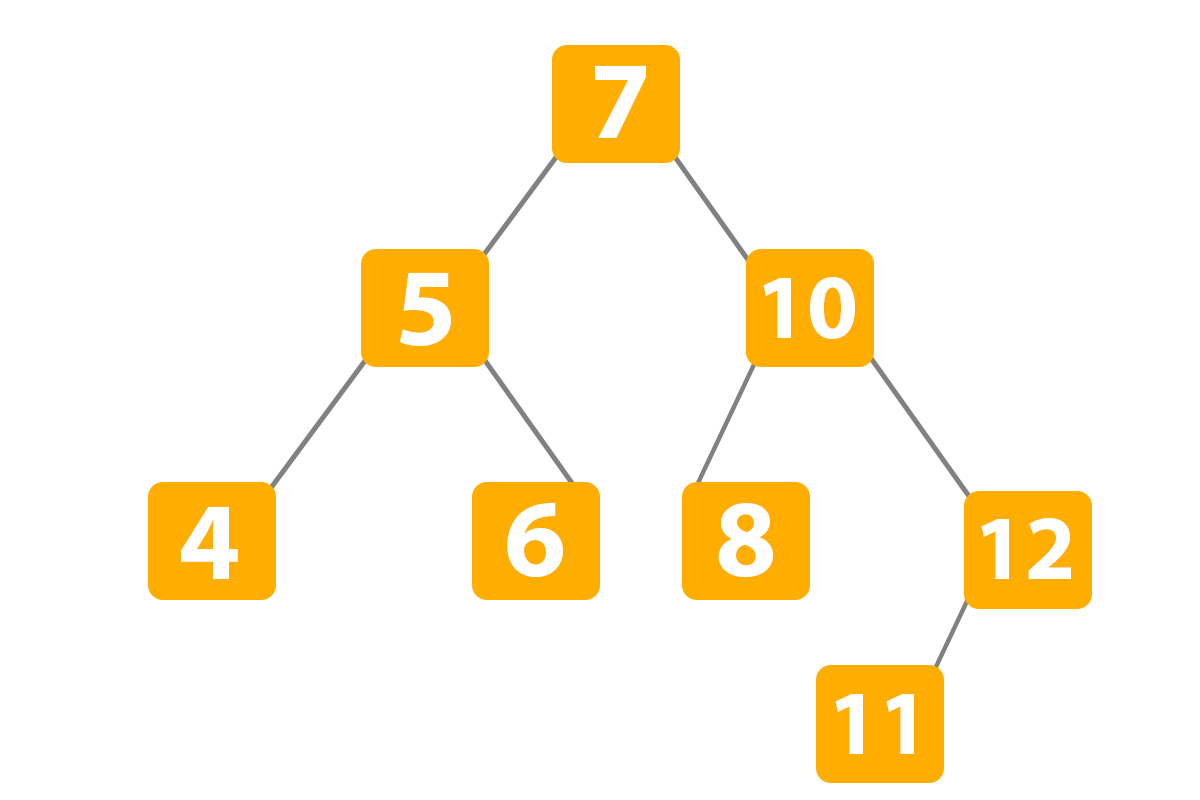
Now, what can we do with a binary search python program? So actually binary tree search Python can be used for storing something like data. The plus will be that it will be organized so you can without a doubt insert something, delete, and update. And also these operations will be as fast as lightning. As we said before BST can provide binary tree search complexity that is called Big-O of O(log(n)) when you are searching, updating or deleting data. Actually linear O(n) is slower than log(n) and it needs some time to find elements. And fact says that a lot of productions use binary trees in their databases like MySQL or PostgreSQL to speed them up when they use CRUD operations.

There are basic operations that you can perform on a binary search tree. Here is the binary search tree implementation. Below we will show basic operations that you can use with a binary search tree.

Let’s create a binary tree python. Tree node class python code can be used as a pointer so you can point to a root node that will connect to the child nodes. Here is the binary tree program in python:

class ExampleNode:
    def __init__(self, value=None):
        self.left_child = None
        self.right_child = None
        self.value = value

Here we will have a value that can function as a key. Also in the line of tree in python code:’value=None’ we can see that if a value will not be created, it will count as None. And in the next two lines, we create two child nodes that equal ‘None’.

Linear search in Python Binary search tree

Binary search algorithm in python depends on the quality of the Binary search treе that all of the left subtrees have values below the root node and all of the right subtrees have values above the root node.

Searching in Python for a value in a binary tree involves comparing the incoming value with the nodes. If this value is below the root node, it means that the value is not in the right subtree, so the search will take place in the left subtree accordingly if this value is above the root node, it means that the search will take place in the right subtree.

So now, let’s try to show steps on how it works. We are finding the number ‘11’:

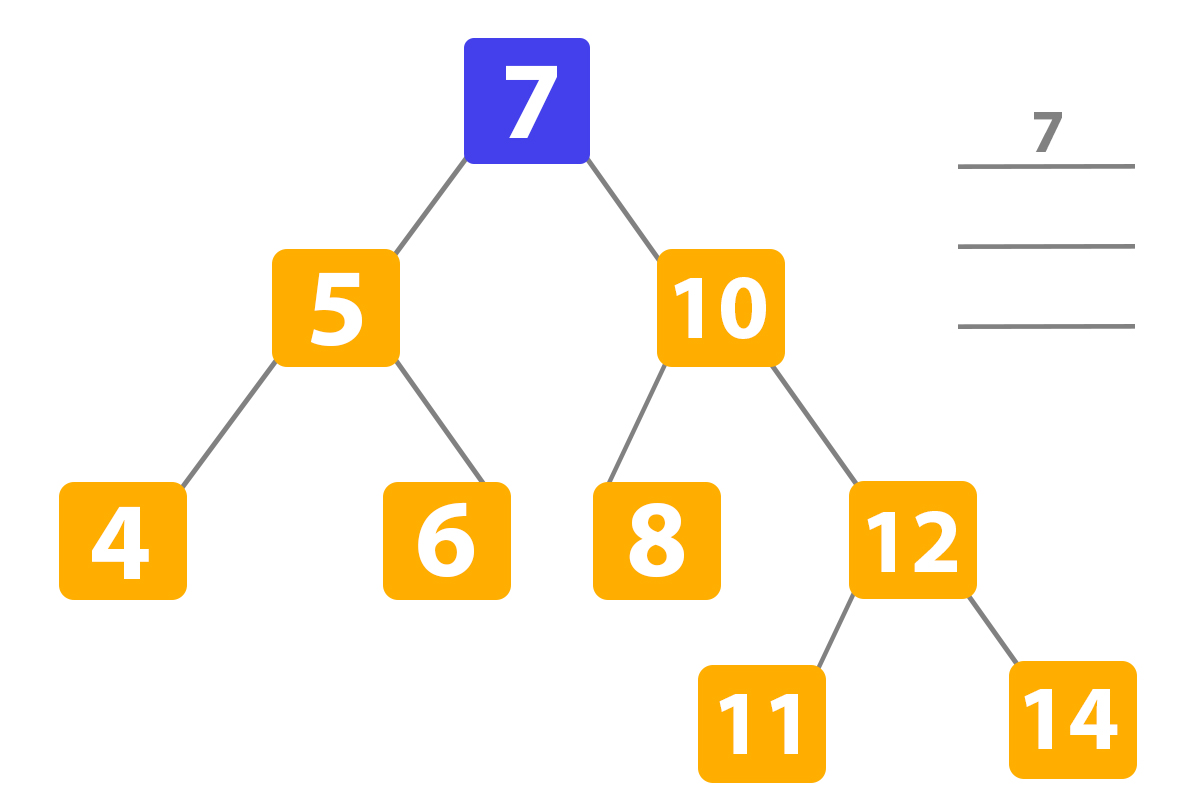
Here our search method in Python has not found the number eleven, so it transfers to the right subtree to find it:

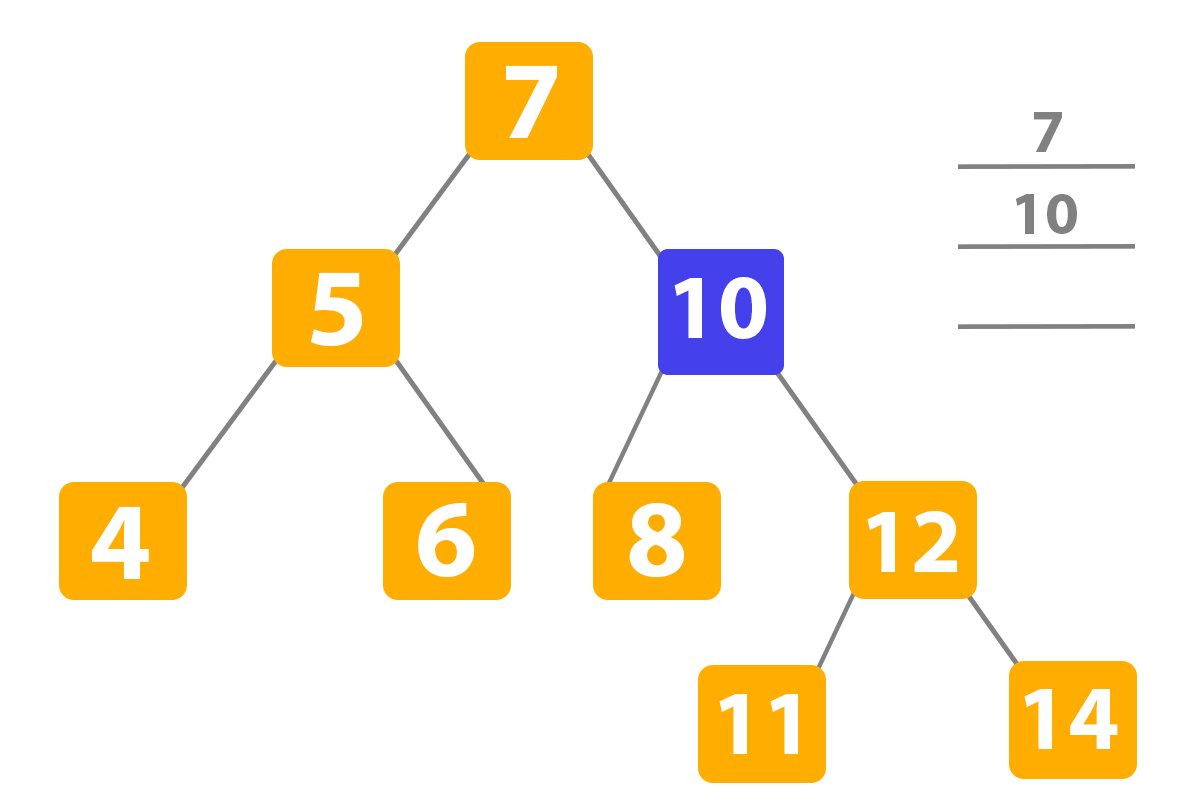
Our search program in python has not found the number eleven here, so it transfers to the right node again because ‘10’ is a higher number than eleven:

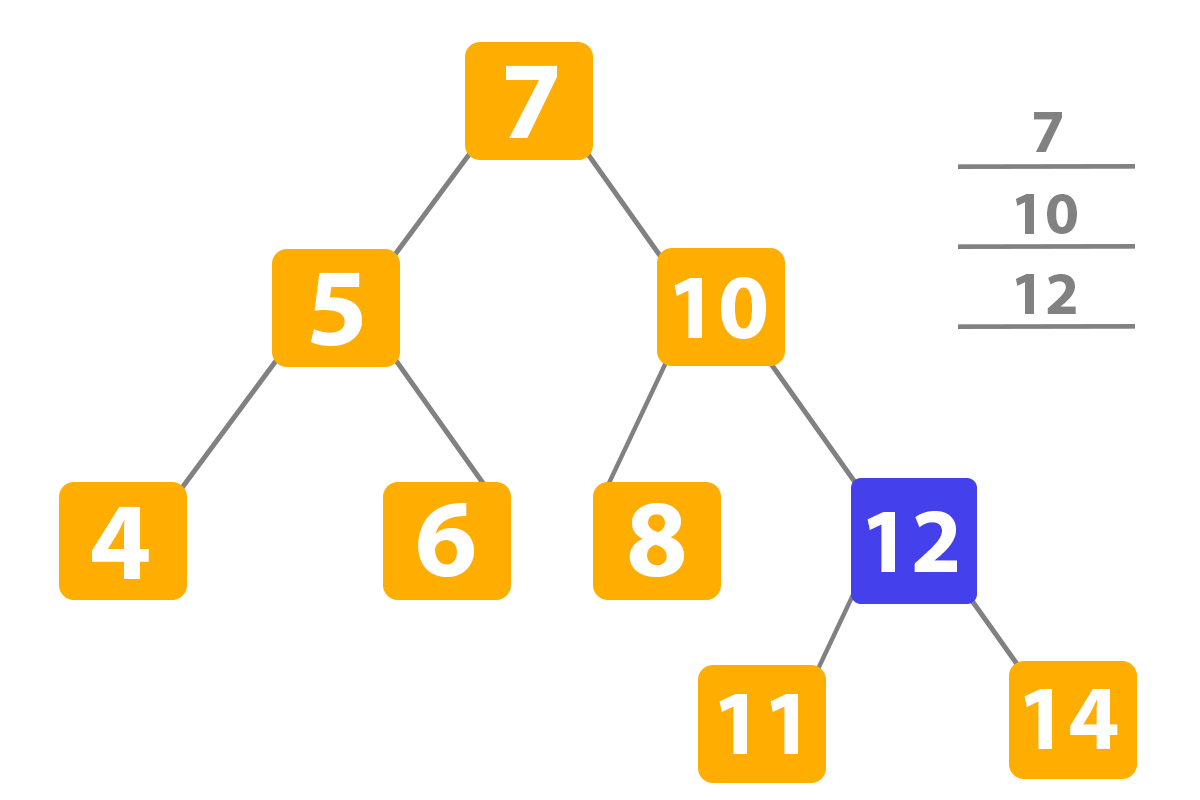
The search program in python has not found again the number ‘11’, and the number ‘12’ is higher than ‘11’ so it transfers to the left subtree:

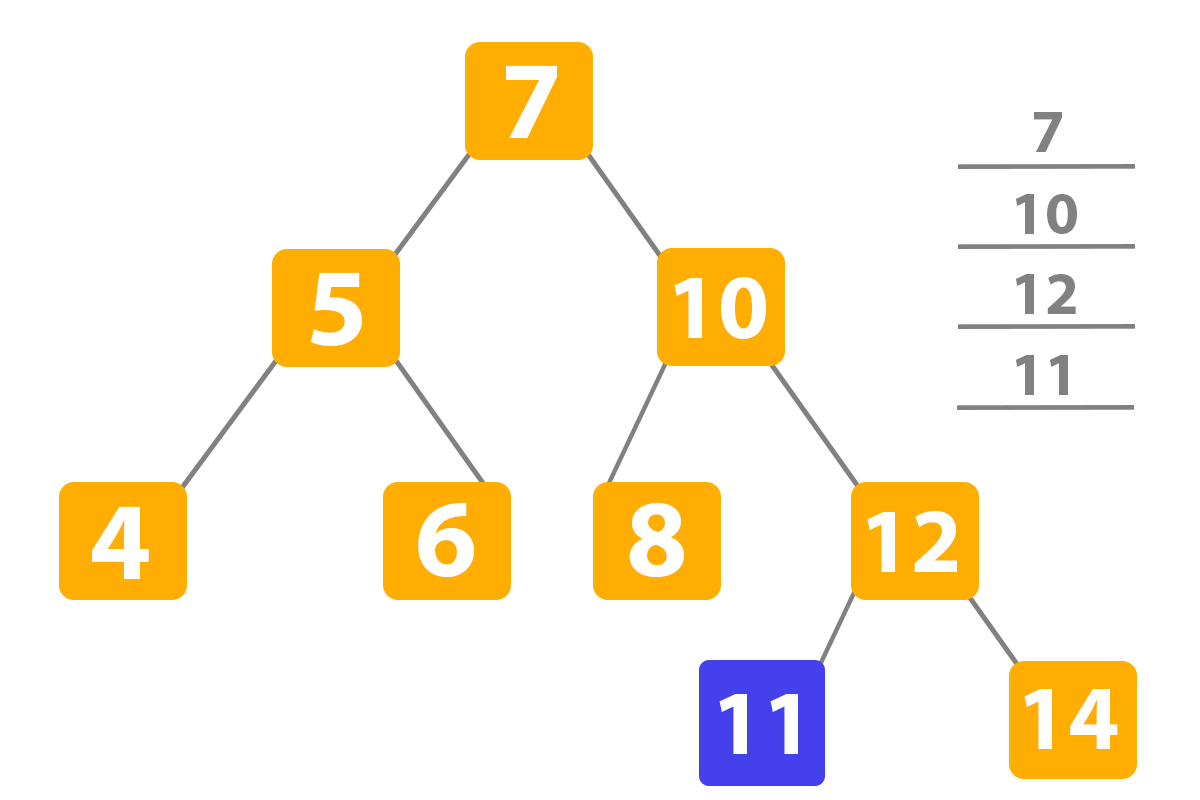
Finally, the number ‘11’ was found. Well done, binary tree search!

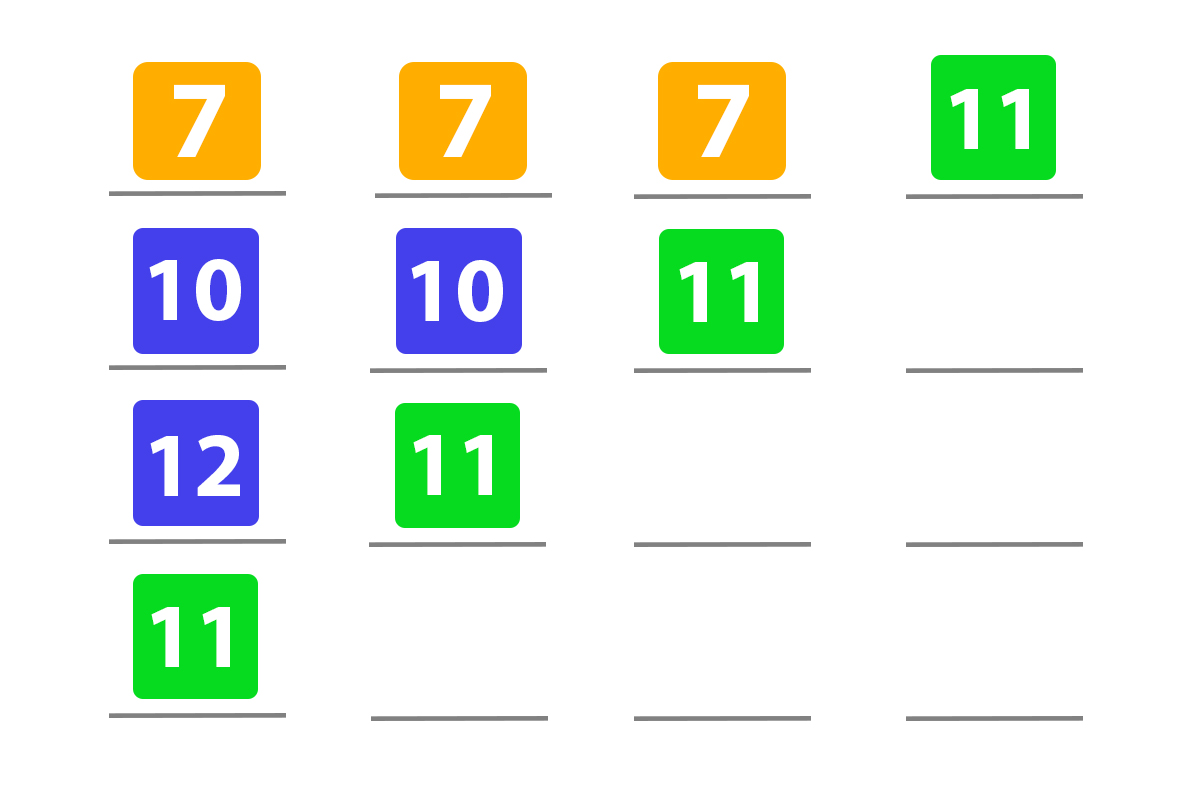
When the binary tree in Python finds our value, it returns. The returned value will spread in every step, so that means that if there will not be, for example, ‘12’, it will find it anyway. In situations when a binary tree can not find the value you need, it returns NULL. Here are the binary search algorithm steps:

Let’s write a program for binary search in a data structure.

class ExampleNode:
    def __init__(self, value=None):
        self.left_child = None
        self.right_child = None
        self.value = value

def search_operation(self, value):
    if value == self.value:
        return True

    if value < self.value:
        if self.left_child == None:
            return False
        return self.left_child.exists(value)

    if self.right_child == None:
        return False
    return self.right_child.exists(value)

So here we see the easy search code in python that returns the boolean value True or False. Binary search python code tree depends on whether the value that we want to find exists or not.

Insert operation in Python Binary search tree

When we want to insert something, for example, a value, we use the same technique as searching because we obey the only rule that in the right subtree there must be larger values and in the left subtree there must be lower values than in our root node.

So the insert technique differs from searching in putting the new node. It looks like that we go through each subtree depending on the value and we put the new node when the left or right subtree is NULL.

Example of binary tree code in python:

If node_root == NULL 
    return createNode(data)
if (data < node_root ->data)
    node_root ->left = insert(node_root ->left, data);
else if (data > node_root ->data)
    node_root ->right = insert(node_root ->right, data); 
return node_root ;

So now, let’s try to show steps on how it works. We are going to add the number ‘11’:

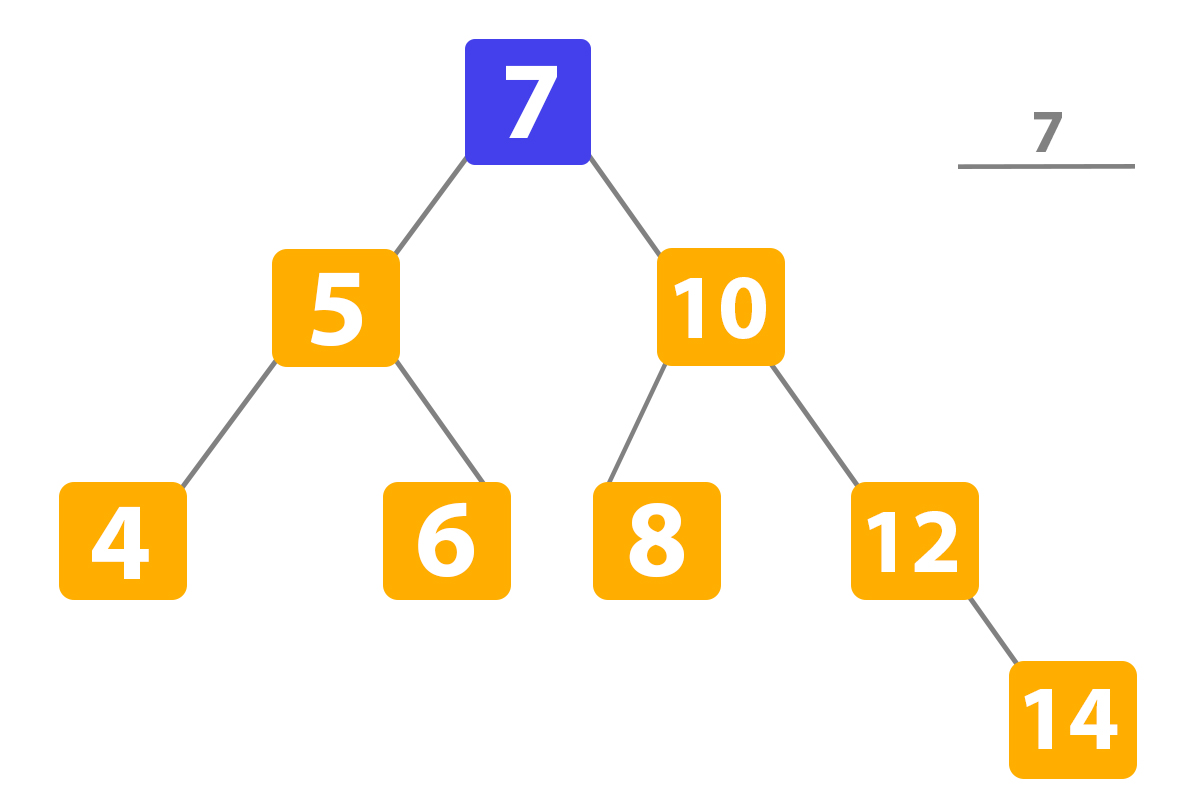
Here we can see that ‘11’ is higher than our root ‘7’ so the Python binary search program transfers to the right subtree:

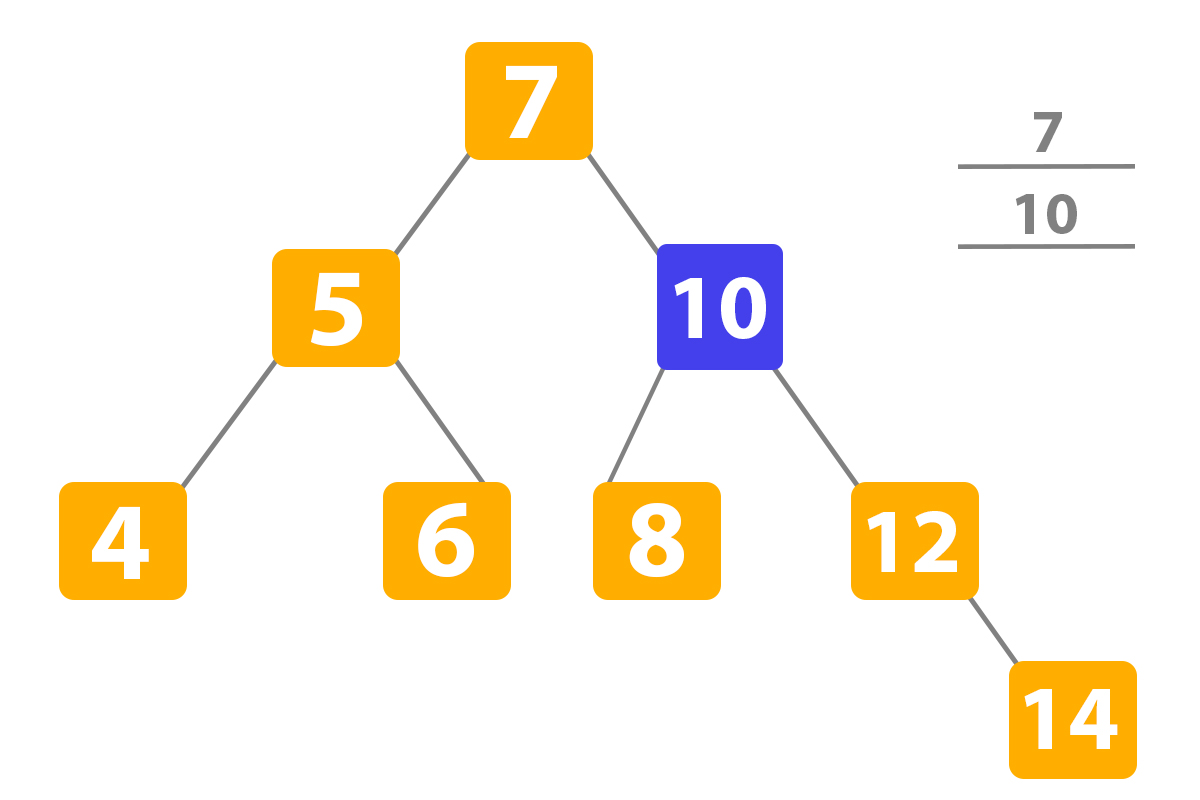
Now again ‘10’ is higher than ‘11’ so we transfer to the right:

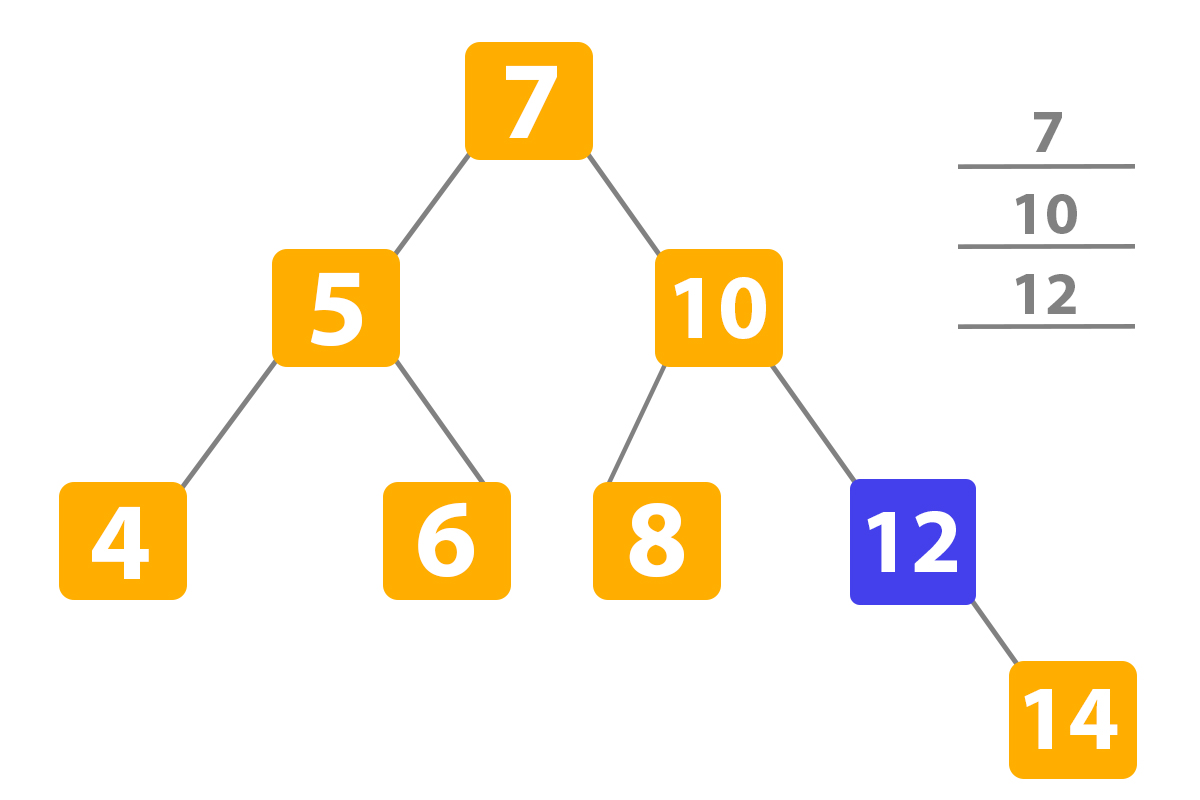
Here is the last transfer, because the number ‘11’ is lower than ‘12’ so which means we’re gonna transfer to the left subtree. And we see that the left subtree is NULL so we add ‘11’ here. Hooray!

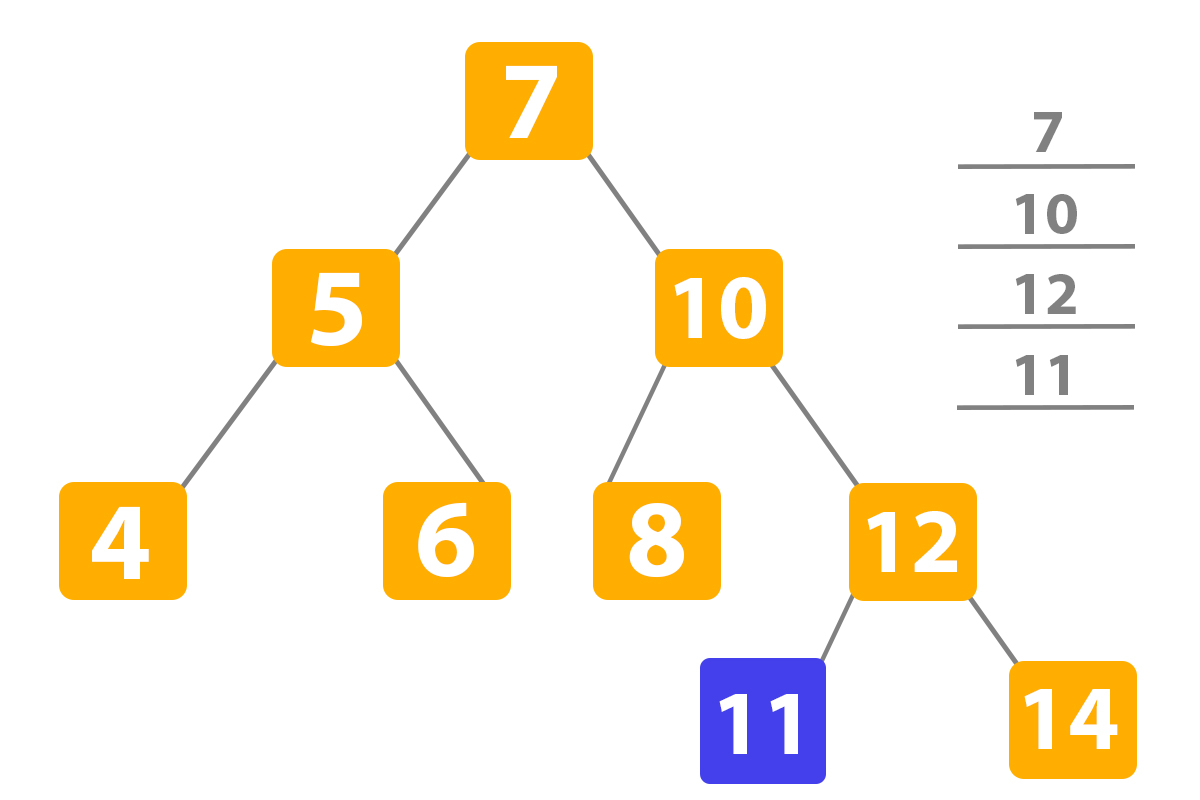
So we put the node with the number ‘11’, but we did not exit the operation, because we needed to return the value. So here the return node comes in hand. The process of returning a node works when we have NULL and create the new node that is returned and attached to the parent node. If we have not found the position for a new node, we without change come back to the root in reverse order.

That means that we move in reverse order in the tree without changing other connections.

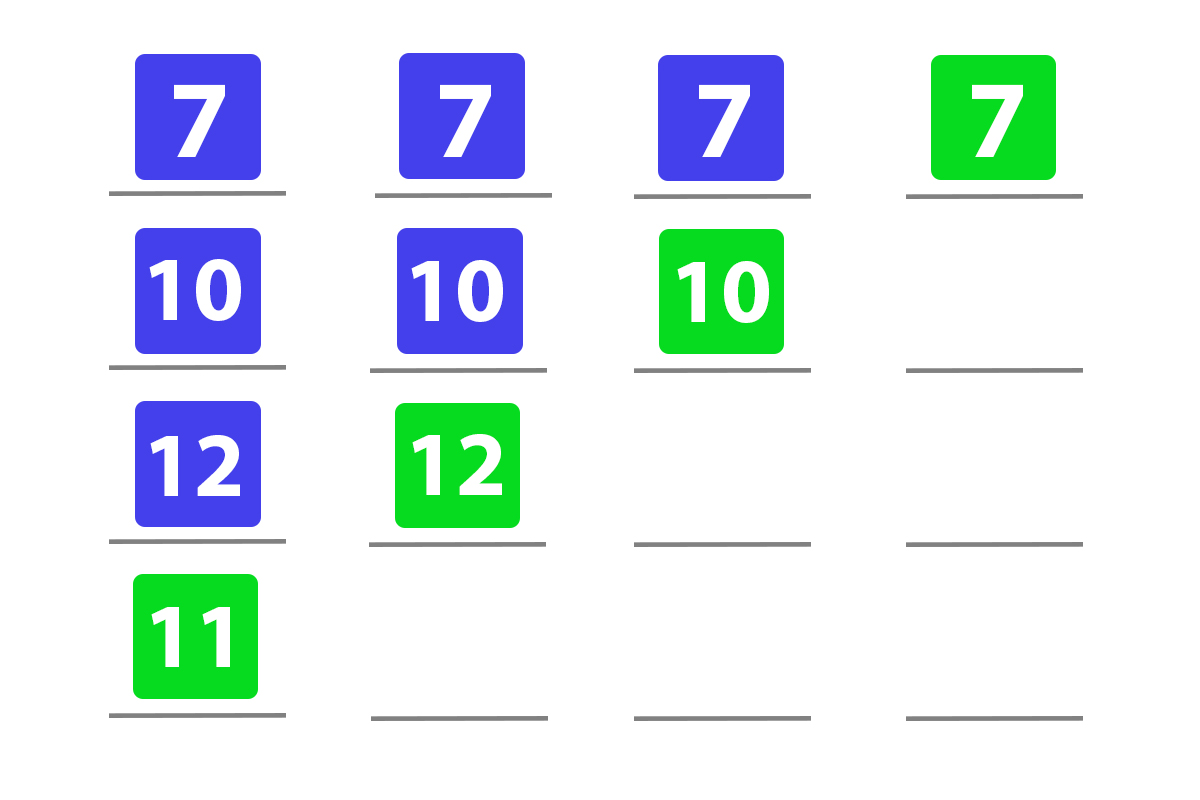
Here we see how in each step we come back to the root without changing any value.

Also, let`s try to create a Python binary search code for this operation:

class ExampleNode:
    def __init__(self, value=None):
        self.left_child = None
        self.right_child = None
        self.value = value

def insert_operation(self, value):
    if not self.value:
        self.value = value
        return

    if self.value == value:
        return

    if value < self.value:
        if self.left_child:
            self.left_child.insert(value)
            return
        self.left_child = ExampleNode(value)
        return

    if self.right_child:
        self.right_child.insert(value)
        return
    self.right_child = ExampleNode(value)

Here we see that we created a python program for binary search where the given value sets and returns if the node does not own a value. But if our node contains the value, it returns it. Also, we used the rule that if the value is lower than the value that is in our node and we have a left child, we recursively call insert on this child. In the opposite case, if we do not have the left child, we just create it with the value that was given. And all the same, is for the right child, but only if our value is higher.

Delete operation in Python Binary search tree

The operation of deleting the node has three variations:

First BST variation:

Binary search in Python program deletes the node that was located in the end of the tree and does not change any connections. For example, we want to delete the number ‘11’:

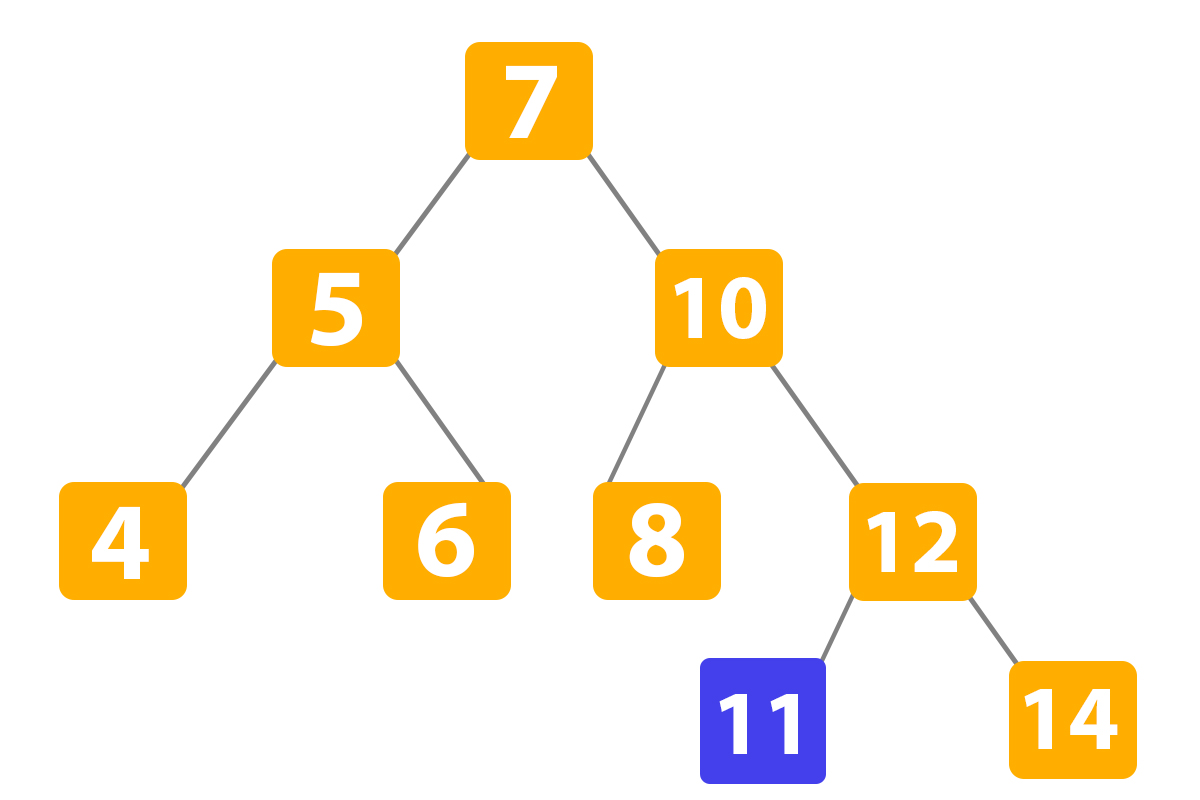
Here python binary search algorithm detected the value and deleted it:

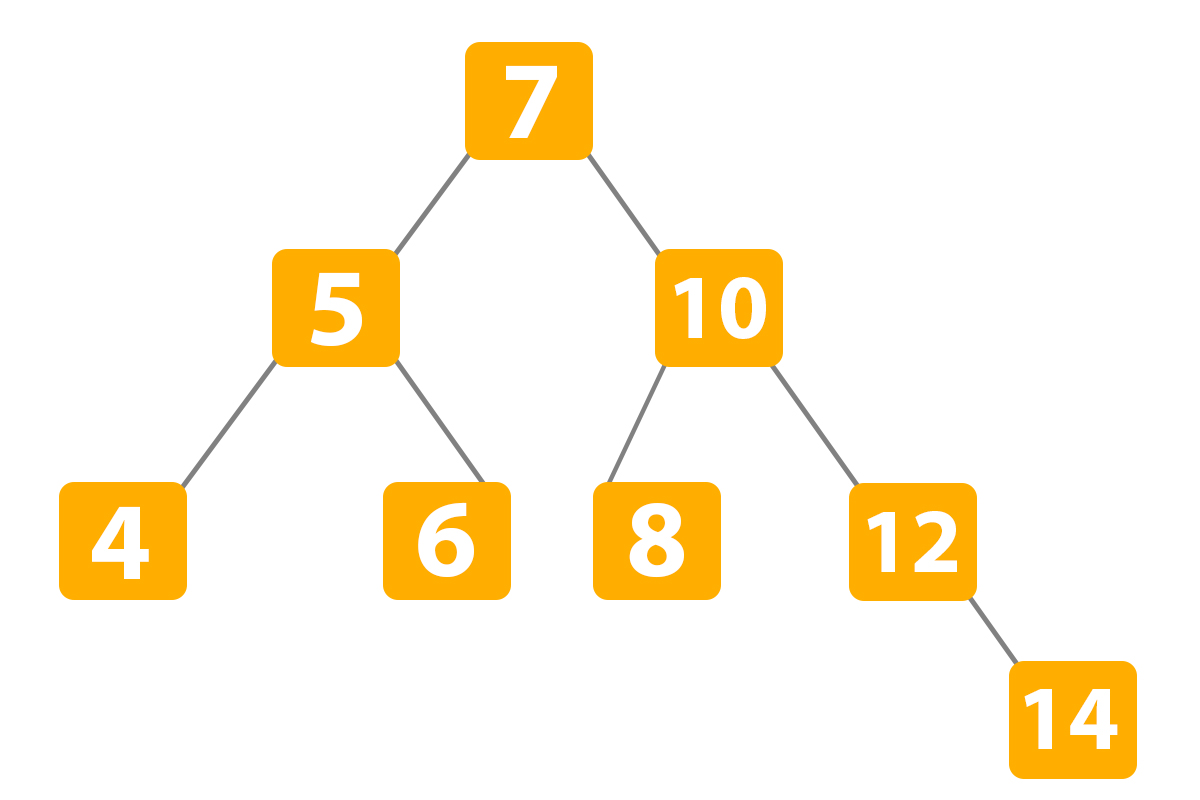
Second BST variation:

When we delete the node that has a child node. For example, we need to delete the number ‘12’:

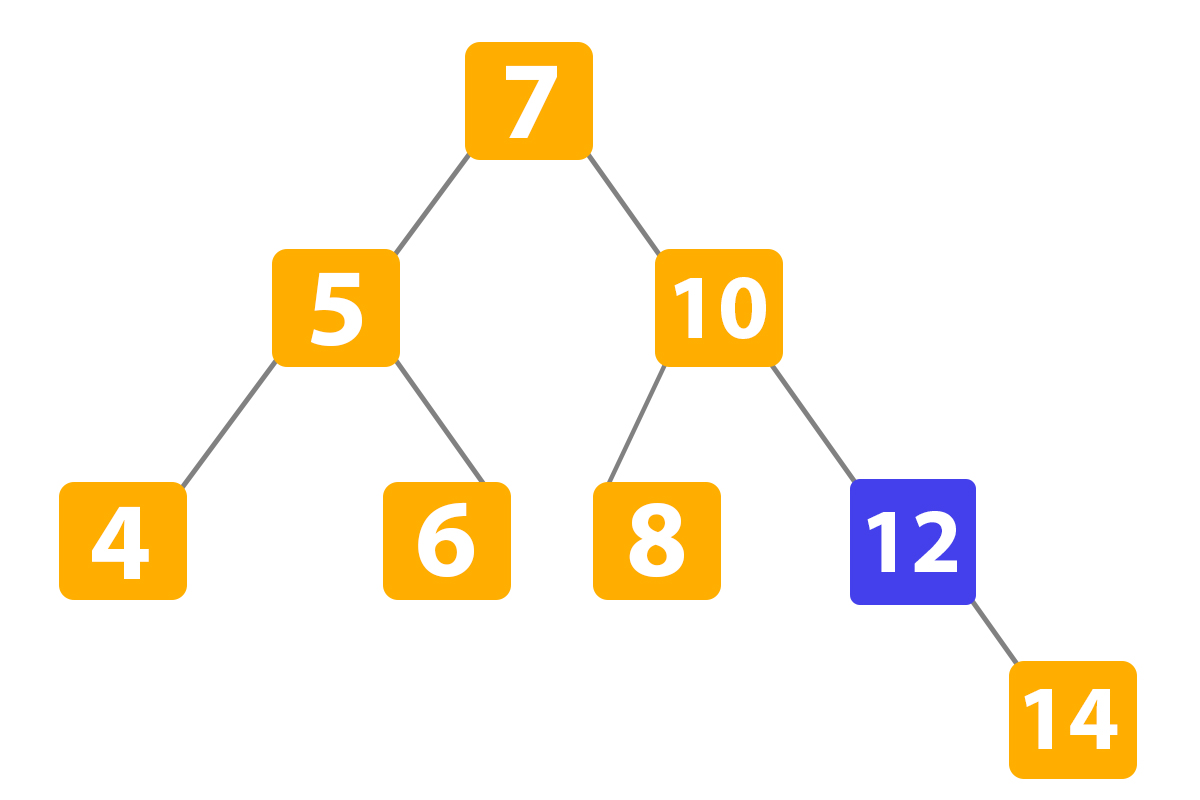
Here we detected the number ‘12’. Next, we copy the value of its child. Our child is number ‘14’. So we copy this value:

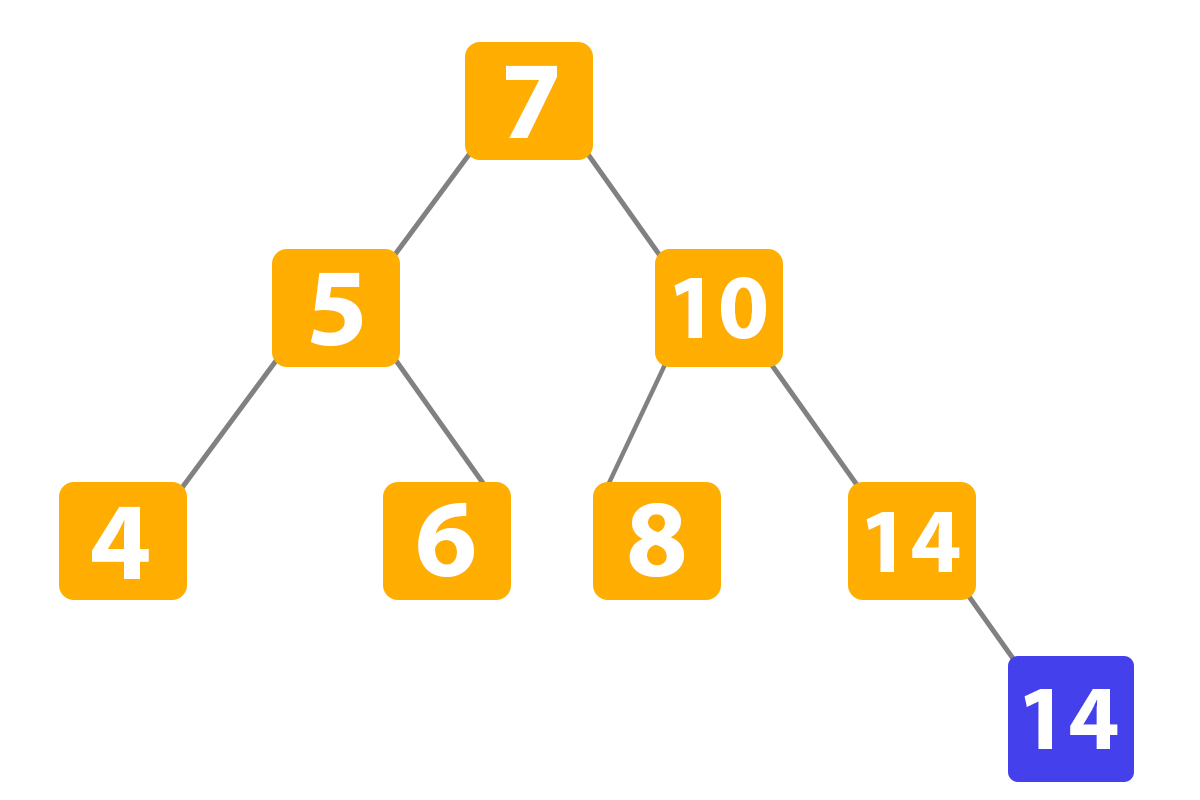
We have already copied the child ‘14’.Then we do the same step as in ‘First variation’, we delete the last node:

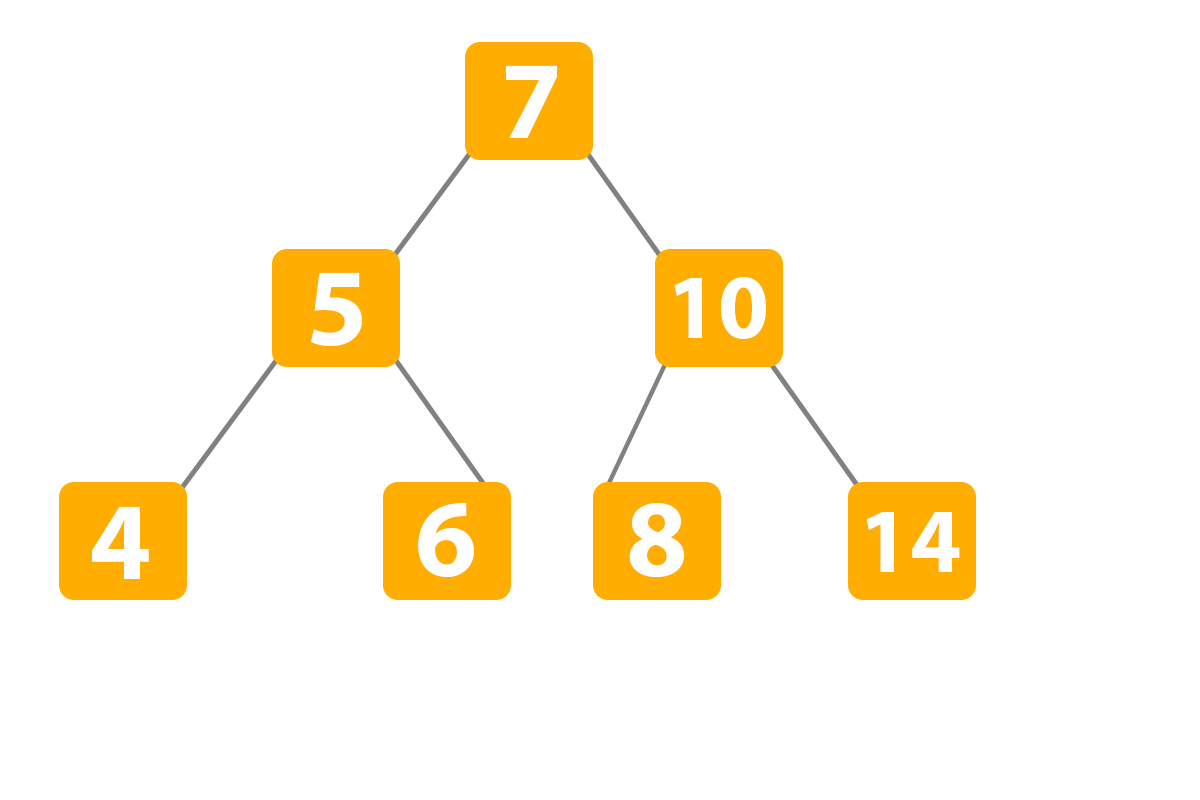
Third BST variation:

When we have more than one child below the node we are searching for deleting. For instance, we need to delete the number ‘10’ from the tree:

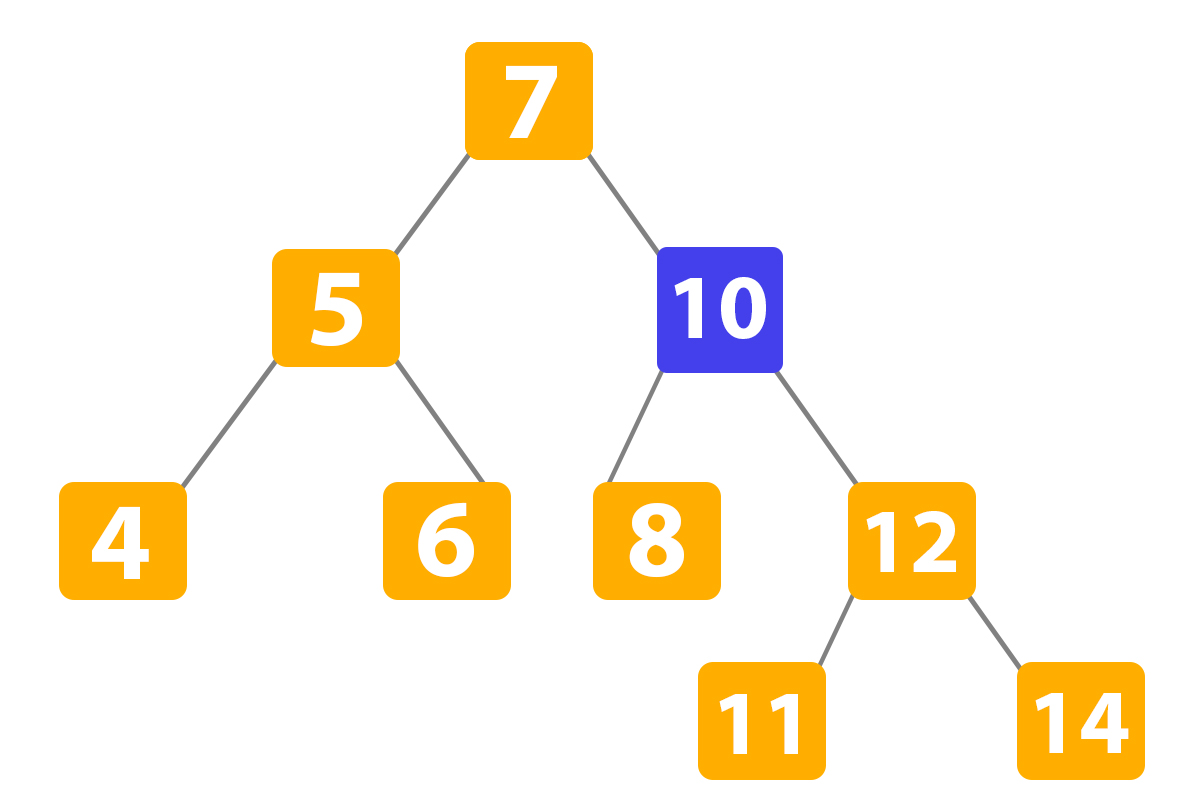
Here we detected the value. Now we must find the successor of the number ‘10’ in the tree. It is ‘11’, so we copy the value:

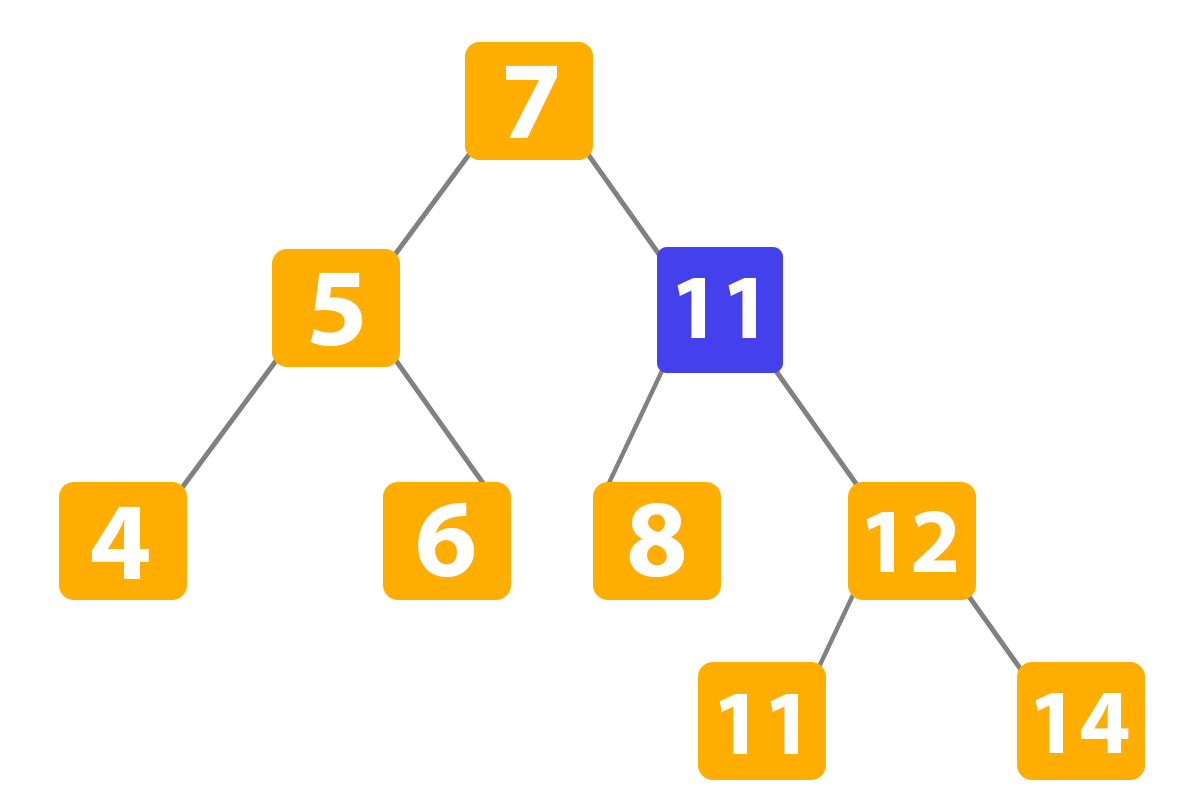
Then we finally delete the node of successor ‘11’:

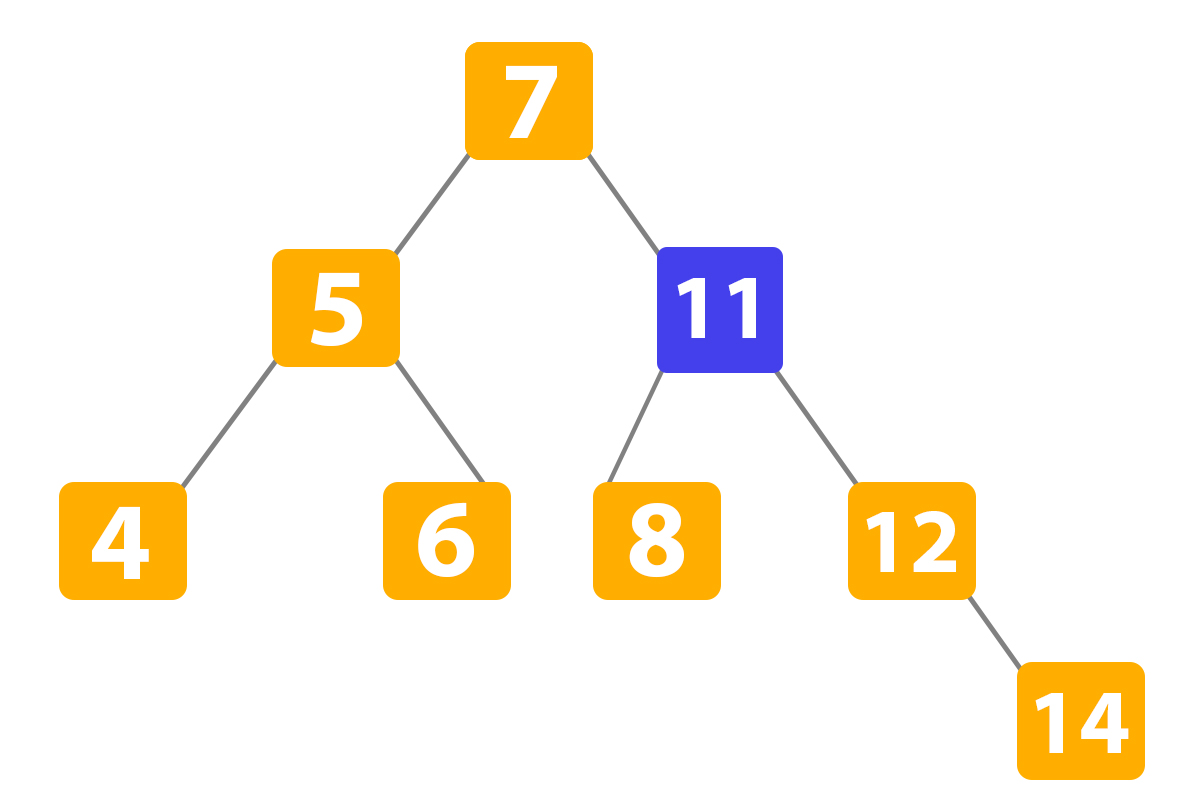
Let’s try to make the program for binary search in python with delete operation:

class ExampleNode:
    def __init__(self, value=None):
        self.left_child = None
        self.right_child = None
        self.value = value

def delete_operation(self, value):
    if self == None:
        return self
    if value < self.value:
        self.left_child = self.left_child.delete(value)
        return self
    if value > self.value:
        self.right_child = self.right_child.delete(value)
        return self
    if self.right_child == None:
        return self.left_child
    if self.left_child == None:
        return self.right_child
    minimum_larger = self.right
    while minimum_larger.left_child:
        minimum_larger = minimum_larger.left_child
    self.value = minimum_larger.value
    self.right_child = 
    self.right_child.delete(minimum_larger.value)
    return selfdef delete(self, value):
    if self == None:
        return self
    if value < self.value:
        if self.left_child:
            self.left_child = self.left_child.delete(value)
        return self
    if value > self.value:
        if self.right_child:
            self.right_child = self.right_child.delete(value)
        return self
    if self.right_child == None:
        return self.left_child
    if self.left_child == None:
        return self.right_child
    minimum_larger = self.right_child
    while min_larger_node.left:
    minimum_larger = minimum_larger.left
    self.value = minimum_larger.value
    self.right_child = 
    self.right_child.delete(minimum_larger.value)
    return selfdef delete(self, value):
    if self == None:
        return self
    if value < self.value:
        self.left_child = self.left_child.delete(value)
    return self
    if value > self.value:
        self.right_child = self.right_child.delete(value)
    return self
    if self.right_child == None:
    return self.left_child
    if self.left_child == None:
    return self.right_child
    minimum_larger = self.right_child
    while minimum_larger.left:
    minimum_larger = min_larger_node.left
        self.value = minimum_larger.value
    self.right_child = 
    self.right_child.delete(minimum_larger.value)
    return self

So here we see this huge tree in Python data structure. But do not worry, it is simple. Actually, this operation works recursively, but it returns the new shape of the node that was given after doing the delete. And it helps in giving access to the parent node whose child node was deleted so we can properly set where the data must be in the left node and where it must be in the right node.

Getting minimum and maximum

with Python Binary search tree

class ExampleNode:
    def __init__(self, value=None):
        self.left_child = None
        self.right_child = None
        self.value = value

def get_minimum(self):
        exact_value = self
        while exact_value.left is not None:
            exact_value = exact_value.left
        return exact_value.value

def get_maximum(self):
    exact_value = self
    while exact_value.right is not None:
        exact_value = exact_value.right
    return exact_value.value

Here we see a very straightforward tree class in Python that can be helpful. They transfer the edges of the data structure tree Python so we can find the largest and the smallest values in our storage.

Why would you need binary trees?

Let’s define a python tree node class. Binary search trees Python can provide very fast O(log(n)) operations that were mentioned before. They are useful for binary sorting in Python. It is very simple to understand and very useful. A simple node class in python without any operations needs only a few lines of code to get to work.

What about the cons? Binary search trees in data structure python are slow for force-brute search. If you want to have iterations through each node, you must better use arrays. Also, BST requires more memory than arrays in implementation.

Actually, there are a lot of appliances where the data tree python will be useful. So the easiest solution to the problem of storing indexes and keys in the database will be BST.

Let’s imagine the example when you need to create a main key column in SQL databases. So here you can without a doubt use a binary python class tree where keys are values in the column and you can point to the rows with nodes. In this situation your SQL base will be easy to search by using keys.

For example, you need to create a game where there must be a list of records of users. It is easy to find the nickname of the user by using binary tree search. And there are more apps where class tree python will be useful. Other simple uses for binary trees you can find in Google.

But what should I use? Binary search in python using list or the binary trees? For this question there are a lot of different answers. They are both positive and negative. Firstly, python node tree use the same pointers to track where the node is as linked lists. But node class python is more efficient and faster while you are searching.